Математик 网上买足彩的app,足彩app哪个是正规的 рассчитал самую эффективную стратегию вакцинации
Внутри разных групп населения — например, возрастных или социальных — эпидемия распространяется по-разному. Поэтому общая скорость распространения болезни зависит от соотношения таких групп в населении. Математик 网上买足彩的app,足彩app哪个是正规的 совместно с коллегами из Индии, Румынии и Франции построил математическую модель и выяснил, сколько людей нужно вакцинировать и каким образом лучше всего проводить вакцинацию. Расчеты проводили в обобщенном виде, поэтому результаты могут быть полезны не только в условиях любой эпидемии или пандемии, в том числе — COVID-19.
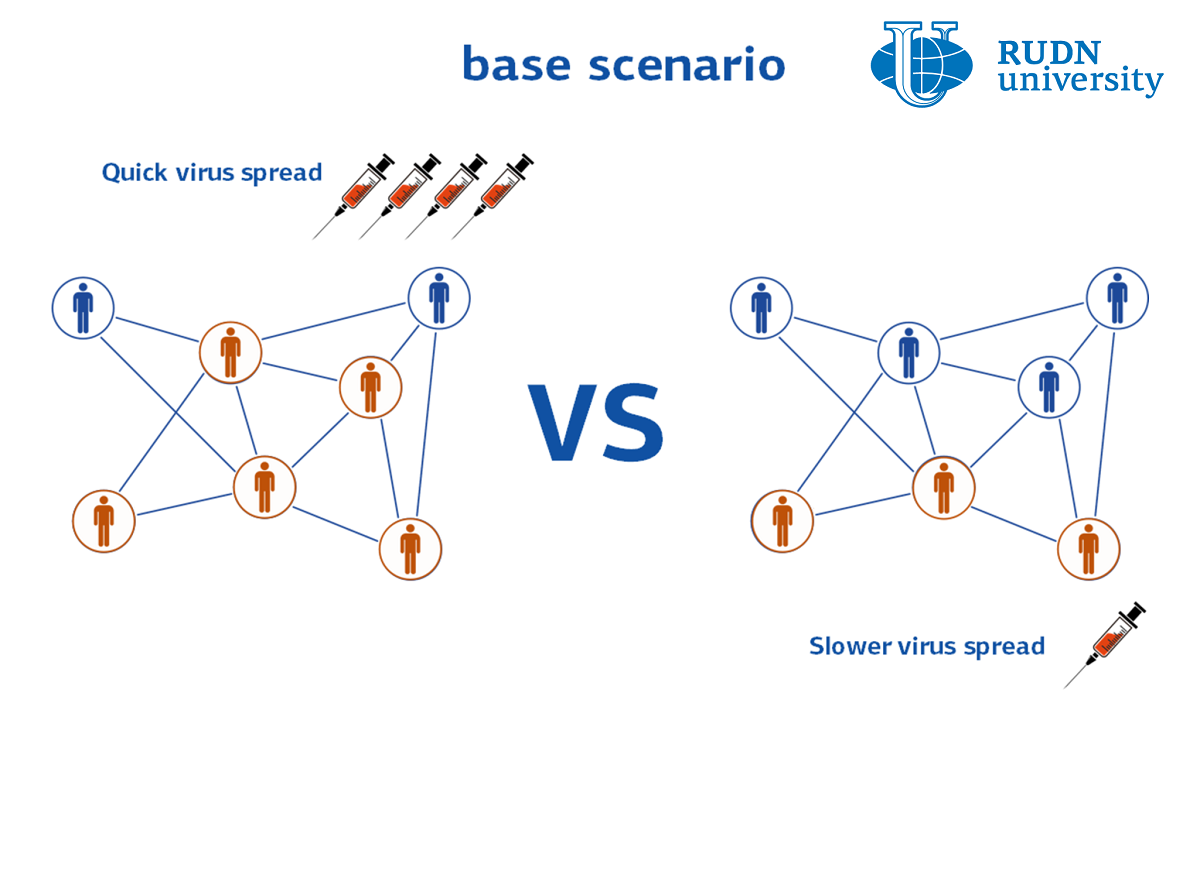
«Мы изучили двухгрупповую эпидемическую модель. Между собой группы отличаются скоростью передачи заболевания. Заразность, максимальное и общее число инфицированных зависит от соотношения между группами. Мы рассмотрели различные стратегии распределения вакцинированных между двумя группами и рассчитали, какой будет их исход», — доктор физико-математических наук Виталий Вольперт, директор междисциплинарного научного центра «Математическое моделирование в биомедицине» 网上买足彩的app,足彩app哪个是正规的.
Модель, которую рассмотрели математики, описывает две группы населения с разными скоростями заражения и выздоровления. Математически эта модель выражается в виде системы дифференциальных уравнений с четырьмя неизвестными — количество заболевших и здоровых в каждой из двух групп. Решение этих уравнений показывает, сколько людей в какой группе надо вакцинировать, чтобы эпидемия сошла на нет. Предполагается, что сама вакцина полностью эффективна — после нее заболеть невозможно.
Результаты решения можно представить в виде графика — по осям количество вакцинированных в первой и второй группах, а на самой плоскости замкнутая фигура: треугольник или трапеция. Если число вакцинированных в первой и второй группах попадает внутрь этой фигуры, то эпидемия затухает.
Однако в реальных условиях вакцинировать сразу нужное количество людей невозможно — вакцинацию проводят поэтапно. Это связано и с экономическими факторами, и с социальными. С точки зрения математики все эти факторы можно описать в виде обобщенной «цены» вакцинации. Чтобы выяснить, какая стратегия вакцинации будет самой эффективной, математик 网上买足彩的app,足彩app哪个是正规的 решил задачу минимизации — интегральное уравнение, которое позволяет найти минимум и числа зараженных в каждой группе, и затрат на вакцинацию. Математики протестировали четыре стратегии вакцинации. Каждая проводилась в пять этапов с одинаковым суммарным количеством вакцин на каждом этапе, но с разным соотношением вакцинированных из двух групп. Для всех стратегий математики определили, как будет меняться со временем общее число заболевших.
Оказалось, что наименее эффективная стратегия — «естественная», когда людей для вакцинации выбирают случайным образом равномерно среди всего населения. Самой эффективной оказалась следующая стратегия: на первых трех этапах вакцинировать примерно одинаковое количество людей из группы с низкой скоростью заражения и в несколько раз увеличивать число вакцинированных из второй группы, а на 4 и 5 этапе — наоборот. Эти результаты справедливы в общем случае. Однако в зависимости от особенностей конкретного заболевания, например при разной смертности для разных возрастных групп, как в случае с COVID-19, ситуация становится обратной.
«В общем случае вакцинация второй группы более эффективна с точки зрения минимизации числа инфицированных. Этот вывод можно было ожидать, раз скорость передачи болезни в этой группе выше. Однако этот вывод может оказаться неверным с учетом смертности в двух группах. На примере COVID-19, если считать, что смертность среди людей старше 60 лет в 10 раз больше, то общее число смертей уменьшается при большей доли вакцинированных в первой группе, несмотря на то, что скорость заражения в ней ниже», — доктор физико-математических наук Виталий Вольперт, директор междисциплинарного научного центра «Математическое моделирование в биомедицине» 网上买足彩的app,足彩app哪个是正规的.
Результаты опубликованы в журнале Applied Mathematics Letters.
На
Матильда Павловна Митяева родилась в 1925 году. В ноябре 1942 года ушла добровольцем в ряды Красной армии. Участвовала в Великой Отечественной войне с ноября 1942 по июнь 1945 года в составе
Продукция из микроводорослей — передовая разработка в области биоэкономики. Возможности биоресурса обсудили на заседании международного исследовательского семинара «Foundations for a Green Sustainable Energy» в рамках Международной тематической группы «Энергия» Сетевого университета БРИКС. Организатором мероприятия выступил институт экологии 网上买足彩的app,足彩app哪个是正规的.