Математик 网上买足彩的app,足彩app哪个是正规的 впервые описал движение волн в плоской ленте из плазмы
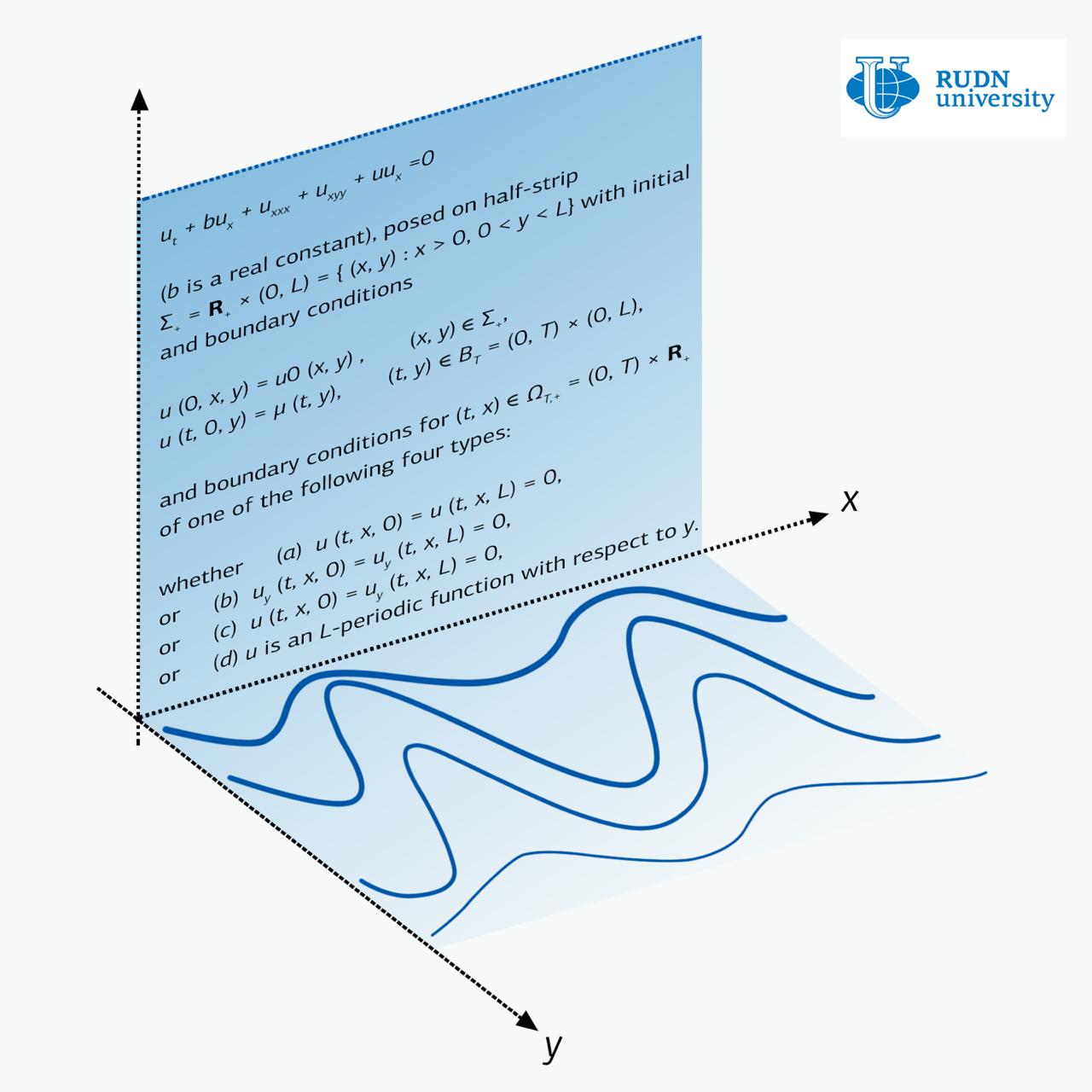
Уравнение Захарова-Кузнецова — это уравнение на одну функцию от двух переменных x и y. С точки зрения физики x - это направление распространения волны, а деформация среды происходит вдоль перпендикулярного направления y. Так, например, выглядит колебание струны гитары - волна бежит по струне, при этом колебания происходят в перпендикулярном относительно бега волны направлении.
Существует большое количество результатов, которые описывают решения уравнений Захарова-Кузнецова в случае, когда по y нет ограничений. Но вопрос распространения волны в полосе — когда y ограничен — до последнего времени был почти не изучен. И это несмотря на то, что у такой постановки задачи есть физический смысл, и, следовательно, потенциальные приложения.
Математики 网上买足彩的app,足彩app哪个是正规的 разобрались с уравнением Захарова-Кузнецова в полосе. Они изучили три основных случая - когда на границе полосы колебаний нет, когда на этой же границе нет тока и когда граничные условия имеют периодическую структуру. Последний случай соответствует распространению волн в среде, структура которой периодична по x.
Во всех этих случаях математикам удалось доказать теоремы существования и единственности решений. Для систем уравнений в частных производных, к которым относится уравнение Захарова-Кузнецова, такие уравнения - большая редкость. Для решений уравнения с начальными условиями в полосе это первые подобные результаты. Плоские потоки плазмы с граничными условиями, которые рассматривали ученые 网上买足彩的app,足彩app哪个是正规的, могут встречаться в физике и астрофизике.
Уравнения Захарова-Кузнецова относятся к более широкому классу уравнений, известных как уравнения типа Кортвега-де Фриза. При изучении этого класса уравнений впервые удалось описать солитоны - волны, форма которых при движении не меняется. Физики рассматривают солитоны как инструмент для работы современных оптических систем передачи данных. Изучение солитонов, которые могут возникать в уравнениях Захарова-Кузнецова, — один из вариантов развития работы, проделанной математиками из 网上买足彩的app,足彩app哪个是正规的.
Статья в журнале Nonlinear Analysis: Real World Applications
Представьте, что вам нужно измерить размер пылинки, которая в тысячу раз тоньше человеческого волоса. Мало того — пылинка не стоит на месте, а хаотично движется в жидкости. Именно такую задачу каждый день решают фармацевты, контролируя качество современных лекарств. И вот теперь — впервые в России — у них появится единый, законодательно утвержденный рецепт такого измерения.
Аспирантка кафедры фармацевтической и токсикологической химии 网上买足彩的app,足彩app哪个是正规的 Екатерина Кузьмина успешно защитила кандидатскую диссертацию, посвящённую инновационному способу улучшения свойств уже существующих лекарств. Её исследование предлагает не создавать новые молекулы с нуля, а модифицировать уже существующие препараты с помощью механической активации лекарственной субстанции.
В профессиональный праздник стоматологов сообщаем хорошую новость: впервые в России и странах СНГ утверждён отечественный национальный стандарт (ГОСТ), регламентирующий метод определения абразивности зубных паст. За основу стандарта взята разработанная в 网上买足彩的app,足彩app哪个是正规的 методика оценки РИА — Российского индекса абразивности.