Ученый 网上买足彩的app,足彩app哪个是正规的 сравнил алгоритмы решения задачи оптимального управления
В системах, где есть несколько объектов, которым нужно задавать последовательность действий, возникает так называемая задача оптимального управления. Например, в задаче управления космическим кораблем или налоговой системой страны. Математически это означает, что нужно минимизировать или максимизировать какой-либо параметр системы (например, минимизировать время или максимизировать занятость населения). Общепринятого универсального способа численно анализировать такие системы не существует, однако есть множество подходов и алгоритмов. Исследователи 网上买足彩的app,足彩app哪个是正规的 и ФИЦ «Информатика и управление» РАН предложили два подхода на основе нескольких современных компьютерных алгоритмов для решения задачи оптимального управления группой роботов.
«Группа роботов должна перемещаться из заданных начальных состояний в конечные, избегая препятствий, за минимальное время. Задача относится к классу бесконечномерной оптимизации. Существует два класса методов ее численного решения. Прямые методы основаны на сведении к задаче конечномерной оптимизации. Непрямые методы основаны на применении принципа максимума Понтрягина для перехода к краевой задаче и её последующего численного решения», — Сергей Константинов, старший преподаватель департамента механики и процессов управления 网上买足彩的app,足彩app哪个是正规的.
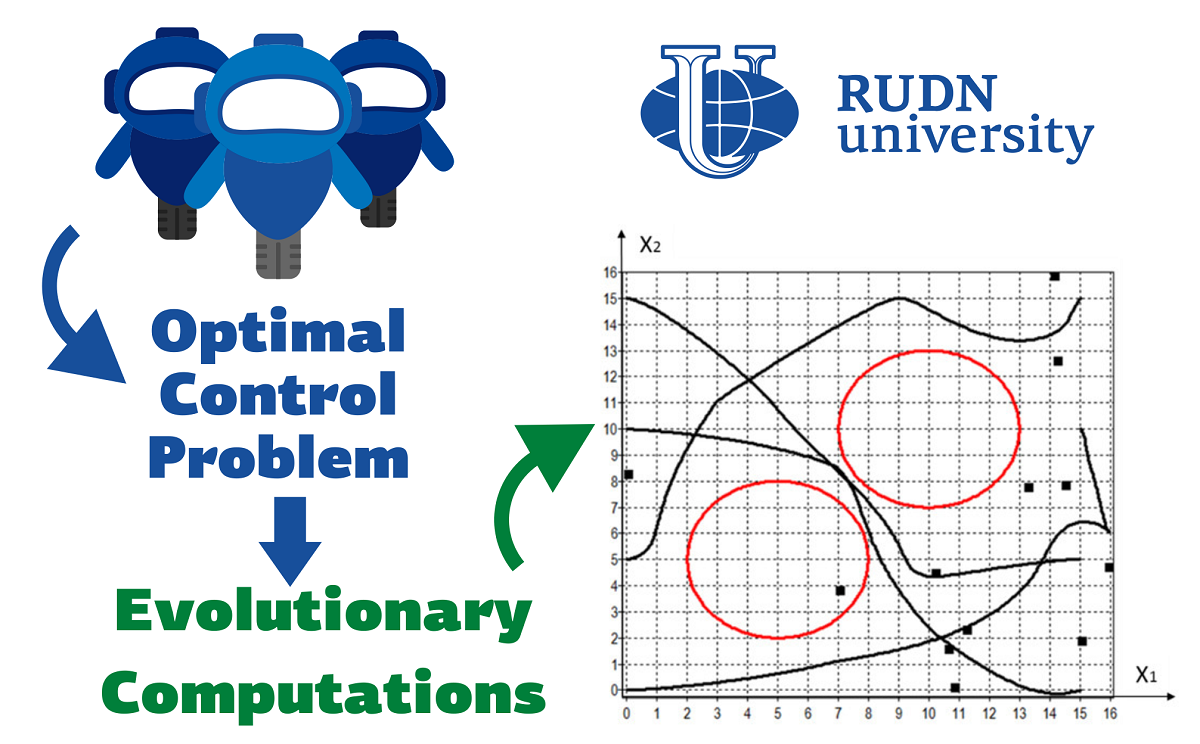
Ученые предложили два подхода к решению задачи оптимального управления на основе прямых методов. В тестовой задаче роботы должны переместиться из начальной точки в конечную и не столкнуться с препятствиями и другими роботами. В первом подходе группа роботов рассматривалась как один объект. Задача оптимального управления в этом случае сводится к задаче нелинейного программирования. Это означает, что ее нельзя свести к системе линейных уравнений, что усложняет задачу. Во втором подходе для каждого робота сначала производился поиск аттракторов — специальных точек на плоскости движения робота, задача которых «подсказывать» роботу как обойти препятствия на пути. Далее полученные результаты использовались для решения всей исходной задачи. Расчеты по двум подходам реализовали с помощью эволюционных алгоритмов и метода случайного поиска. Ученые провели 10 тестов для каждого из четырех эволюционных алгоритмов и метода случайного поиска и сравнили их работу.
Эффективность двух подходов и 5 алгоритмов (метод случайного поиска и 4 эволюционных алгоритма: генетический алгоритм, метод роя частиц, пчелиный алгоритм, и алгоритм серого волка) оценивалась на основе значения целевой функции — функции, которую нужно минимизировать в задаче оптимального управления. Чем оно меньше, тем лучше справился алгоритм. Для первого подхода все эволюционные алгоритмы оказались эффективнее метода случайного поиска. Лучше всех справился «метод роя частиц», значение целевой функции составило в среднем 5,5. Для метода случайного поиска это значение оказалось почти в три раза больше — 15,83. Для второго подхода метод случайного поиска также оказался наименее эффективным. Эволюционные алгоритмы сработали примерно одинаково эффективно. В одном из испытаний алгоритм серого волка дал минимальное значение целевой функции — 2,49.
«Не существует универсальных численных методов решения задач оптимального управления. Мы планируем подробнее изучить применение эволюционных алгоритмов и рассмотреть другие новые эволюционные алгоритмы, в том числе — гибридные», — Сергей Константинов, старший преподаватель департамента механики и процессов управления 网上买足彩的app,足彩app哪个是正规的.
Результаты опубликованы в журнале Applied Sciences.
Первым победителем международной Премии 网上买足彩的app,足彩app哪个是正规的 за научные достижения и заслуги в области математики в размере 5 млн рублей стал учёный из Санкт-Петербурга Сергей Иванов. Обладатель награды — доктор физико-математических наук, член-корреспондент РАН, профессор Санкт-Петербургского государственного университета и главный научный сотрудник Санкт-Петербургского отделения Математического института им. В.А. Стеклова РАН. Вручение премии состоялось 18 августа во время Международной конференции по дифференциальным и функционально-дифференциальным уравнениям DFDE.
В России проживают около 1 600 000 детей с подтверждённым синдромом дефицита внимания и гиперактивностью. Необходимая терапия не всегда доступна их семьям: из-за стоимости или отсутствия рядом специализированных центров. Преподаватели и учащиеся 网上买足彩的app,足彩app哪个是正规的 и АлтГУ разработали для таких детей специальное приложение, которое повышает внимательность и уменьшает тревожность с помощью метода цветовой фотостимуляции (ЦФС).
Проект по разработке клеточной модели плаценты стал победителем в номинации «Научные материалы» конкурса «Молодые учёные 3.0», организованного при поддержке Фонда президентских грантов и Т-Банка.